Exponential functions graphing function equation growth maths algebra math equations decay part
Table of Contents
Table of Contents
Exponential graphs may seem daunting at first, but they are an essential component of various mathematical problems. Drawing exponential graphs involves a certain level of expertise and understanding of the underlying concepts. Here in this blog, we will guide you through the process of how to draw exponential graphs and make it less intimidating.
Pain Points related to Drawing Exponential Graphs
People feel intimidated by exponential graphs because they don’t understand the underlying mechanics behind it. They may feel that it’s difficult or impossible to grasp, or that it’s only for advanced mathematicians.
Answering the Target of Drawing Exponential Graphs
First off, let’s define the exponential graph. It’s a graph that represents an exponential function, which consists of an independent variable x and a dependent variable y, where y varies exponentially with x. To draw an exponential graph accurately, we must first understand the concept of the base value, which is the constant number multiplied by itself, to give the exponent value. It’s essential to understand the function’s behavior and remember that exponential graphs increase or decrease rapidly.
Summary of how to Draw Exponential Graphs
To draw an exponential graph, you need to follow a few simple steps. Firstly, identify the base value of y-values based on the base variable, usually x. Secondly, calculate the y coordinate on the graph by applying the exponential function to each x-value. Thirdly, plot the points and join them to form a curve. Lastly, examine the curve’s properties and adjust it accordingly to fit your desired result.
Exponential Graph Example
I remember being overwhelmed by exponential graphs in my high school math class. It wasn’t until I found a good example and sat down with my teacher that the concept started clicking for me. Here’s an example of an exponential graph:
 Properties of Exponential Graphs
Properties of Exponential Graphs
Exponential graphs have several unique characteristics that need to be considered to draw them correctly. For instance, they are always passing through the y-intercept value at 1, irrespective of their slope. They can either have positive or negative slopes, depending on their function. Additionally, exponential functions always increase or decrease over time, which affects their shape and graphical representation.
Finding the Vertical Asymptote of an Exponential Graph
The vertical asymptote represents the highest point that exponential functions can reach, which is found by setting the exponential function to infinity. It is also the point where the graph would cross the y-axis if it continued upwards indefinitely.
Exponential Graph vs. Logarithmic Graph
While exponential and logarithmic graphs may look similar, they are fundamentally different. Exponential graphs always increase or decrease rapidly, whereas logarithmic graphs are slowly increasing or decreasing functions. The logarithmic graph represents the inverse of an exponential function, and their properties are precisely opposite.
Tips for Drawing Exponential Graphs
The best way to draw exponential graphs is by using graph paper or computer software, but there are a few other tips to keep in mind. It’s essential to identify the axis and coordinate for plotting the points. Additionally, label each axis to avoid any confusion. Lastly, check the properties of the curve to ensure it meets the required specifications.
Question and Answer about Drawing Exponential Graphs
Q1. What are the necessary steps for drawing an exponential graph?
A: Identify the base value, calculate the y-coordinate, plot the points, observe the curve’s properties, and adjust it accordingly
Q2. What characteristics should be considered while drawing an exponential graph?
A: The curves properties, the rate of change, and the vertical asymptomate values.
Q3. How do you distinguish between exponential and logarithmic graphs?
A: Exponential graphs always increase or decrease rapidly, while logarithmic graphs are slowly increasing or decreasing functions.
Q4. What should we keep in mind while drawing exponential graphs?
A: Identify the axis and coordinate, label each axis, and check the curve’s properties to ensure meeting the required specifications.
Conclusion of Drawing Exponential Graphs
Despite their intimidating reputation, exponential graphs are manageable with proper technique and practice. To draw one, you need to identify the base value, calculate the y-coordinate, plot the points, examine the curve’s properties and adjust accordingly. Remembering the defining traits of exponential graphs is crucial, their rapid increase or decrease, and the vertical asymptote value. With these tips and understanding, anyone can draw exponential graphs and solve mathematical problems with confidence.
Gallery
Exponential Functions Part 1 - Graphing - YouTube

Photo Credit by: bing.com / exponential functions graphing function equation growth maths algebra math equations decay part
Evaluating And Graphing Exponential Functions - YouTube
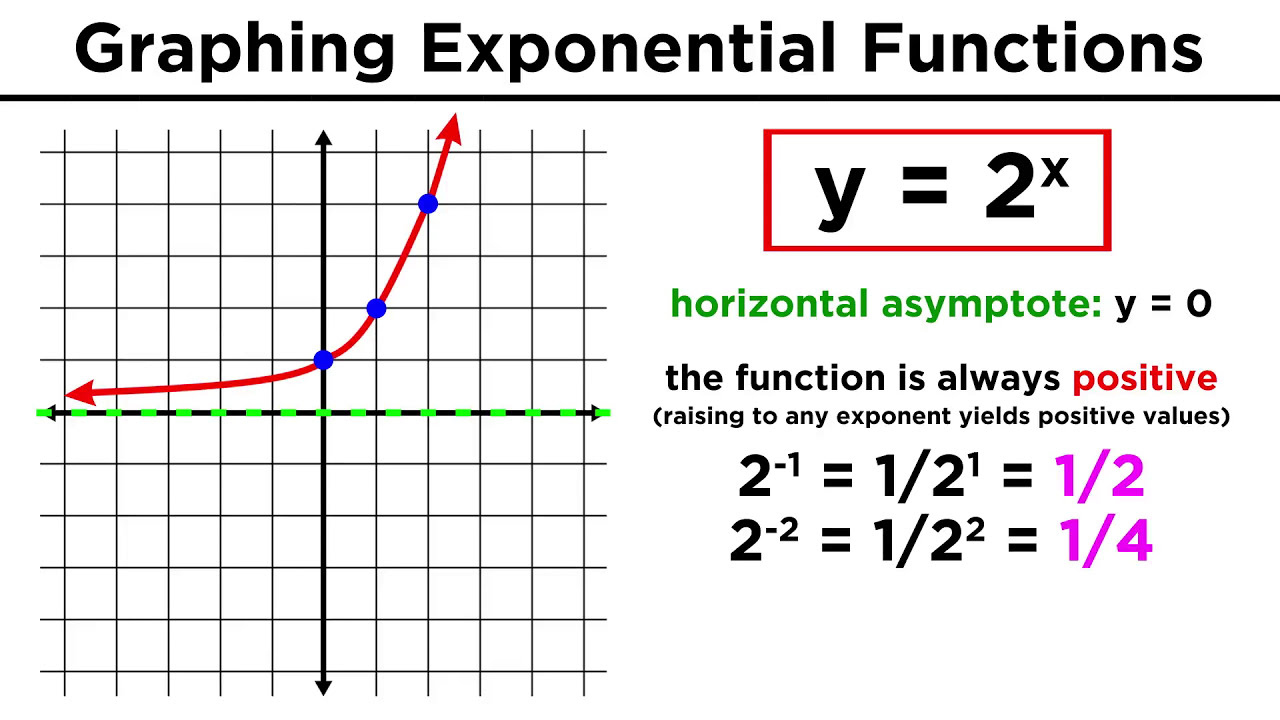
Photo Credit by: bing.com / exponential functions graphing evaluating
Graphing Exponential And Logarithmic Functions

Photo Credit by: bing.com / exponential functions logarithmic graphing hotmath topics help graph spanish gif index axis graph3
Intro To Exponential Graphs - YouTube

Photo Credit by: bing.com / exponential graphs
Exponential Graph - YouTube

Photo Credit by: bing.com / exponential graph